Сибирская С.Н.

Ретестовое исследование двух авторских опросников Таланова В.Л.

В исследовании использовались два опросника: на 579  и 584 вопроса. Эти наборы состоят из разных вопросов и  обрабатываются единой методикой, автором которой является В.Л. Таланов. Эти наборы с расчетными таблицами были любезно предоставлены Талановым В.Л. в не эксклюзивное пользование  для научных исследований. Инициатива, исполнение и юридическое сопровождение данного проекта принадлежит С. Сибирской. Авторское право на опросники и расчетные таблицы принадлежат Таланову В.Л.

 Сбор анкет производился с 22 января по 27 марта 2015 года, и было собрано по 445 анкет каждого опросника. Тесты – опросники имеют условные названия IOSG579 (содержит 579 вопросов) и ССТ584 (содержит 584 вопроса).

Сходимость версий ТИМов между  тестами

Тесты дают по три ближайших ТИМа, каждый из которых имеет свой рейтинговый номер: 1,2,3. Первый номер имеет наибольший вес, остальные соответственно меньший. Первый по номеру называем ведущим типом.

Вначале вычисляем сходимость первых номеров обоих тестов. Затем вычисляем сходимость вторых и третьих номеров с учетом порядка следования и без учета порядка следования.

Первая часть таблицы показывает процент сходимости версий вместе с их номером присутствия. Совпадение первых номеров происходит с частотой 69%. Совпадение первого и второго номера одновременно – с частотой 41% и совпадение 1-го, 2-го и 3-го с учетом порядка следования происходит с частотой 28%.

Вторая часть таблицы показывает сходимость версий без учета порядка следования. Случаи, когда хотя бы одна версия из троек одинакова (вне зависимости от номера следования), встречаются  с 99% частотой. Случаи, когда две версии из этих троек одинаковы, встречаются с 85% частотой. И случаи, когда обе тройки содержат по три одинаковых типа, но могут занимать разный рейтинговый номер, встречаются с 28% частотой.

Детальное сравнение тестов CCT и IOSG

Кроме изучения простого совпадения версий типов, была изучена согласованность тестов по всем основным соционическим факторам. Тесты примечательны тем, что предоставляют детальную информацию по каждому диагнозу.

Корреляционные коэффициенты между тестами по каждому соционическому фактору представлены в таблице ниже.

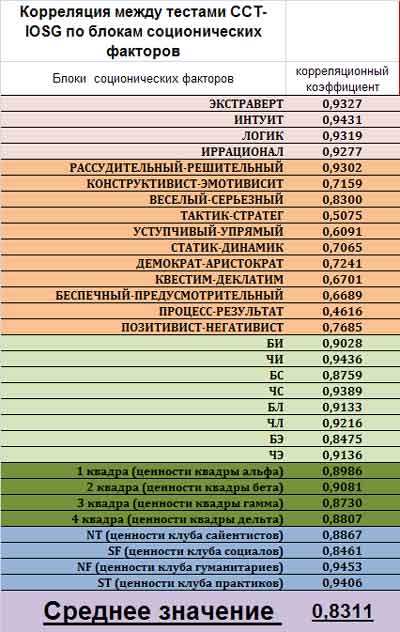
Таблица показывает сверх высокое сходство тестов по основным дихотомиям, функциям, квадрам и клубам. По признакам Рейнина  сходство неравномерное.  Одни признаки показывают высокое сходство (рассудительный, конструктивист, веселый, статик,  демократ, беспечный, позитивизм), а другие – низкое (тактик, процесс).

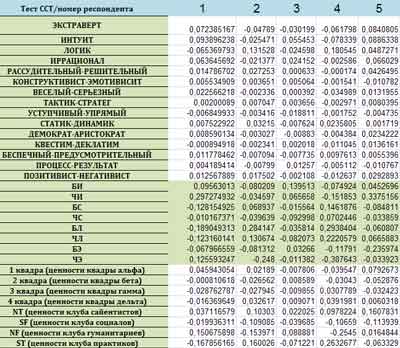
Таблица получена путем вычисления коэффициентов корреляции по горизонтальным рядам, то есть по всем респондентам целиком. Внизу показана часть  таблиц с первичными данными для пяти респондентов. По горизонтали идут респонденты, по вертикали - факторы. Например, для вертности сравнивался ряд «экстраверт» длиной 445 респондентов из таблицы CCT с аналогичным рядом из таблицы IOSG. Коэффициент корреляции получился 0.9304. Это первое число в таблице «Корреляция между тестами CCT-IOSG по блокам соционических факторов». Аналогично были получены корреляционные коэффициенты для остальных факторов таблицы.

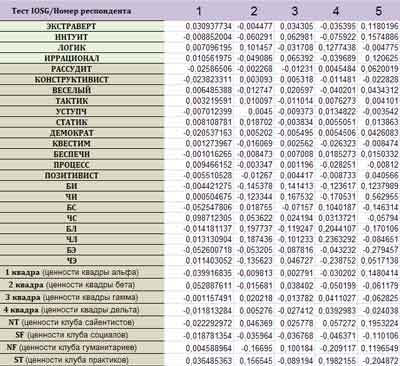
Другой способ вычисления коэффициента корреляции между вертикальными рядами для каждого респондента в отдельности.  Например, берется вертикальный ряд для 1-го респондента, то есть все факторы, представленные в таблице (31 штука), теста CCT и вертикальный ряд теста IOSG и вычисляется коэффициент корреляции. В результате для каждого респондента  вычисляется корреляция между двумя тестами.

На этом рисунке показана часть таблицы, где показаны вычисленные коэффициенты для 5-и респондентов. Среднее значение коэффициента корреляции по 445  респондентам равно  0.8818. Это достаточно хороший результат.

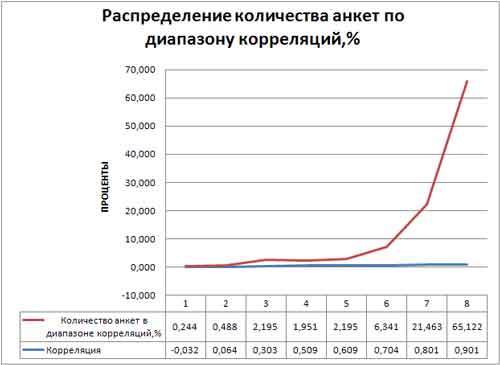
Приводим распределение количества анкет по диапазону корреляций. Корреляцию между двумя тестами от -0.032 до 0.064 имело 0.24% респондентов. Корреляцию в диапазоне от 0.064 до 0.303 получили около 0.5%, далее  в трёх диапазонах присутствовало по приблизительно по 2%. В диапазон от 0.7 до 0.8 попало около 6%, в диапазон от 0.8 до 0.9 попало около 21%, и в диапазон от 0.9 до 1 – 65%. Таким образом, в диапазоне от 0.8 до 1 находится более 86% респондентов. БОльшая часть анкет попадает в диапазон высоких корреляций. Анкет с корреляцией меньше 0.5 всего 5%. Анкет с корреляцией выше 0.5 - 95%.

Мы получили два варианта общих средних коэффициентов корреляции вычисленных двумя способами: 0.8302 и 0.8818. Это показывает, что согласованность двух опросников достаточно высокая.

Сходимость тестов по выборкам надежных и контрастных анкет

Тесты вычисляют некоторые стилевые особенности заполнения анкет. Эти особенности влияют на точность результата типирования. Для исследования были взяты коэффициенты надежности и контрастности.  Выборки были разделены по группам с высокими и низкими коэффициентами надежности и контрастности.

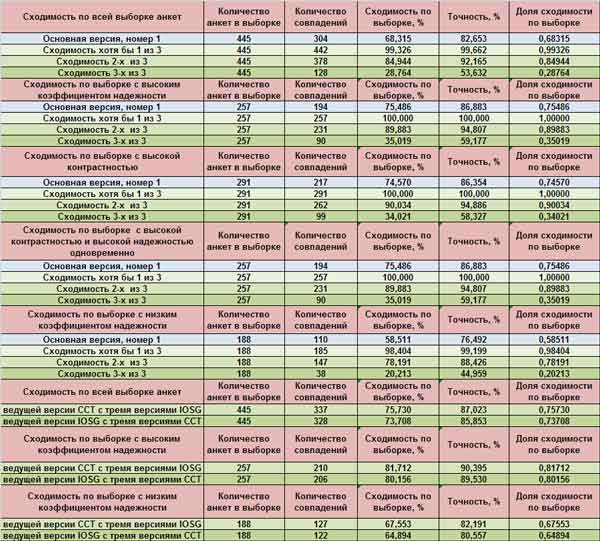
Ниже приведена таблица сходимости для выборок надежных, контрастных, одновременно надежных и контрастных и выборки ненадежных анкет. В последней правой колонке указана точность типирования анкетами. Точность вычислена как корень квадратный из сходимости.

Точность типирования для всей выборки около 83%.  Точность для надежных анкет – около 87%, для контрастных – 86%, для надежных и контрастных одновременно – 87%. Кроме всего прочего была выделена выборка анкет с низким коэффициентов надежности. Для этой выборки сходимость около 58%, а точность типирования около 76%. Эти значения справедливы для основной версии ТИМа, то есть первого номера.

В таблице представлены еще вычисления сходимости для троек ТИМов без учета порядка следования по всем группам выборок. Интересный результат для случая «сходимость хотя бы 1 из 3-х» равный 100%. Этот результат имеет место для выборок надежных и контрастных анкет. Как это понимать? Это значит, что если коэффициент надежности высокий, то одна из трех версий, выданная одним тестом с вероятностью 100% встретится в тройке версий другого теста.

И даже для ненадежных анкет эта вероятность достаточно велика  и равна 99.2%.

Высокие значения корреляции между тестами ССТ и ИОСГ говорят о хорошей внутренней согласованности методики.  Ретестовое исследование показало высокую повторяемость  результатов: от 70 до 100%.

Заключение

1. Произведено одновременное типирование двумя опросниками Таланова В.Л. 445 респондентов.
2. Основная версия на выборке 445 респондентов без изъятий повторялась в 68% случаев, что говорит о точности типирования 83%.
3. Для надежных анкет основная версия повторялась в 75% случаев. Для ненадежных анкет основная версия повторялась в 58% случаев.
4. Точность типирования надежных анкет около 87%, а ненадежных-76%.
5. Тройка наиболее весомых версий  с вероятностью 98-100% содержит версию, которая повторится в следующем тесте. Можно предположить, что именно эта версия будет окончательной..
6. Тесты показывают очень высокое (0.87-0.95)  сходство по основным соционическим факторам: дихотомиям, функциям, клубам, квадрам.
7. Вывод. Высокая повторяемость диагнозов доказывает утверждение, что тесты Таланова самые надежные из всех ныне существующих.

Светлана Сибирская. 2015.

Приложение. О вычислении точности.

Математические основания вычисления точности. Под понятием точности подразумеваем вероятность выдачи точного (истинного, верного) диагноза ТИМа. Предположим, что точность некоторого теста Х. Это значит из сотни протипированных Х штук получат верный диагноз, а 100-Х ошибочный. То есть точность это отношение верных диагнозов к общему количеству протипированных. Точность измеряется от 0 до 1. В таблице эта доля правильных диагнозов переводится в проценты умножением на 100.

Задача 1. Предположим мы имеем два теста с известной точностью Х1 и Х2. Тогда сходимость между этими тестами будет равна произведению их точностей.

С=Х1*Х2

Например.

Точности Х1=0.5, Х2=0.8, тогда С=0.5*0.8=0.40, переводя в проценты получаем 40%

Точности Х1=0.7, Х2=0.8, тогда С=0.7*-0.8= 0.56, умножая на 100, получаем сходимость 56%.

Если точности равны Х1=Х2=0.7, С=0.7*0.7=0.49, переводя в проценты получаем сходимость 49%.

Задача 2. Обратная задача.

Мы имеем два теста с неизвестной точностью, но знаем сходимость между ними.

С=0.81=Х1*Х2

Мы не можем точно решить эту задачу, но можем сделать прикидку первого приближения, предположив, что точности одинаковы. Тогда точности будут равны корню крадратному из сходимости.

Если С=0.81, то Х1=Х2=корень из 0.81=0.9 или в процентах 90%. Точность 90%.

Если С=0.49, то Х1=Х2=корень из 0.49=0.7 или в процентах 70%. Точность 70%.

В таблице приведены именно эти прикидочные точности тестов. Поскольку тесты имеют одну и ту же методику, то предположительно точности близки.